2
剰余の定理のおかげで,実際に割り算(多項式の割り算はめんどくさい!)をしなくても P (2) P(2) P (2) を計算するだけで余りが求まりました。 このように 剰余の定理 とは,多項式を (x − a) (xa) (x − a) で割ったときの余りを素早く計算するための定理です。反射テスト 整数 整式の割り算と余り 01 1 2 つの自然数m;n がある m は12 で割ると商がa で余り5;
割り算の商と余り a-b
割り算の商と余り a-b-具体的には,整式の割り算における商と余りは,次のように計算できる. 例 A(x) = 3x4 2x3 x2 4x 5,B(x) = x2 2x 1とする.このとき,A(x)をB(x)で 割ったときの商と余りを求めよ. 解 整数の割り算と同じような方法を用いて,次のように計算できる. x2 2x 1 多項式の割り算、商と余りの求め方をみていきます。 1変数xの2つの多項式A(x), B(x)を考えます。多項式の係数は全て整数とします。 次数の大きい方をA(x), 次数の少ない方をB(x)とし、 ここでは次数の少ない方の多項式の最大次数の係数は1としておきます。
剰余の定理
R のとき, (1) 割り算の中を見ると A BQ=R だから A=BQR が成り立つ. (余りはかけ算に参加しない.) (2) 数の割り算では,割る数が取り除ける限り取り除くので,余りは割る数よりも小さい. 多項式の割り算では,割る式よりも次数が低くなるまで 割り算の基本公式 を用いれば、 等式 を導くことができます。 両辺はともに同じ整式であるはずなので、等式は 恒等式 となるはずです。 問題では、 割り算の基本公式から導いた等式が恒等式である ことを利用して、定数の値や商を求めることになります。 割り算の基本 割り算は「 除法 」とも言い、 割り算の結果を 「 商 」と呼びます。 「 除 」には「 取り除く 」という意味があり、「 割り算 」とは「 いくつ取り除けるか 」という事です。 「 商 」は、むかし 商人 たちが「 自分たちの分け前や取り分を、はかる時 」に使っていたという説も
「quotient」は和差積商の商でした。商とは割り算の答えを指しています。 この表現も足し算や引き算でも同じなので覚えておくと良いでしょう。 割り算の余りは「remainder」 足し算、引き算、掛け算にはない表現として「余り」というものがあります。 整数の割り算と商および余りの説明のおわりに いかがでしたか? 割り算に関する式は「割られる数 = 割る数 × 商 余り」の形で表すということは必ず覚えておきましょう。 また上式の右辺を用いて、余りによる分類を行うことができるという点について算数の余り(あまり)とは、割り算をしたとき、割り切れず余った数のことです。 例えば、37÷7は割り切れません。 但し、37÷7=5・・・2のように、余り「2」を付け加えて、商を表すことができます。 今回は、数学の余り、意味、記号と表し方、商、除法
割り算の商と余り a-bのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
「割り算の商と余り a-b」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
「割り算の商と余り a-b」の画像ギャラリー、詳細は各画像をクリックしてください。
整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
「割り算の商と余り a-b」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 | 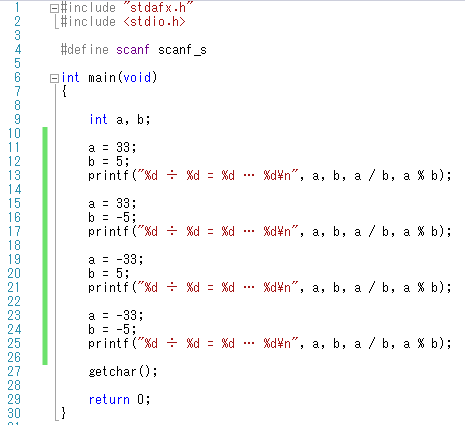 整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
「割り算の商と余り a-b」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
「割り算の商と余り a-b」の画像ギャラリー、詳細は各画像をクリックしてください。
整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
「割り算の商と余り a-b」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 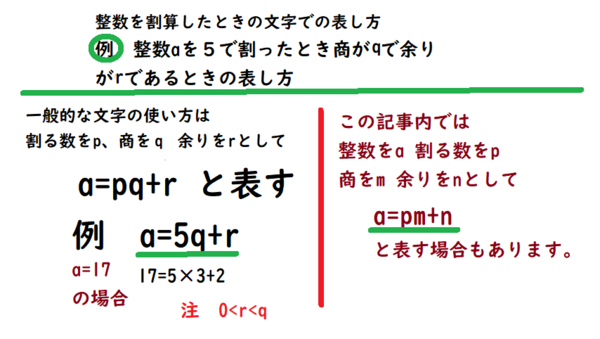 整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
「割り算の商と余り a-b」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 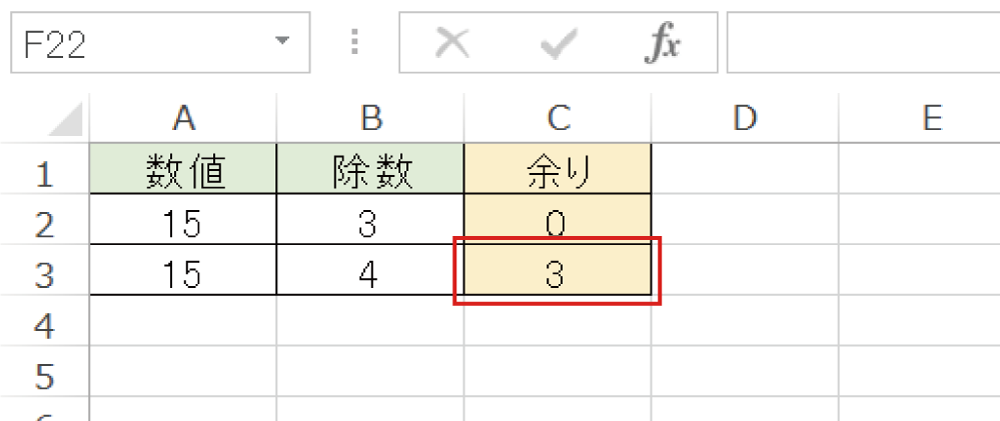 整数の割り算における商と余り 例題で学ぶ高校数学 |
「割り算の商と余り a-b」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
「割り算の商と余り a-b」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
「割り算の商と余り a-b」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
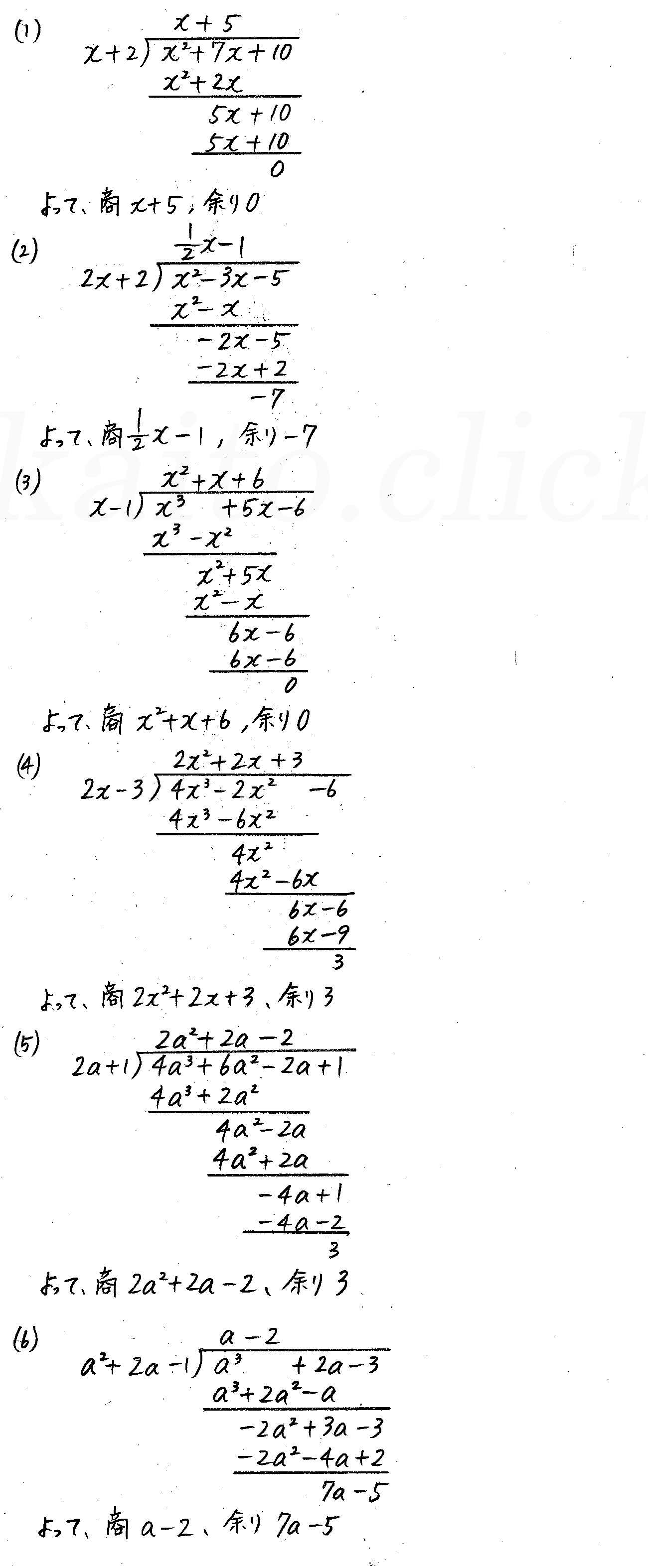 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
「割り算の商と余り a-b」の画像ギャラリー、詳細は各画像をクリックしてください。
 整数の割り算における商と余り 例題で学ぶ高校数学 |  整数の割り算における商と余り 例題で学ぶ高校数学 | 整数の割り算における商と余り 例題で学ぶ高校数学 |
 整数の割り算における商と余り 例題で学ぶ高校数学 |
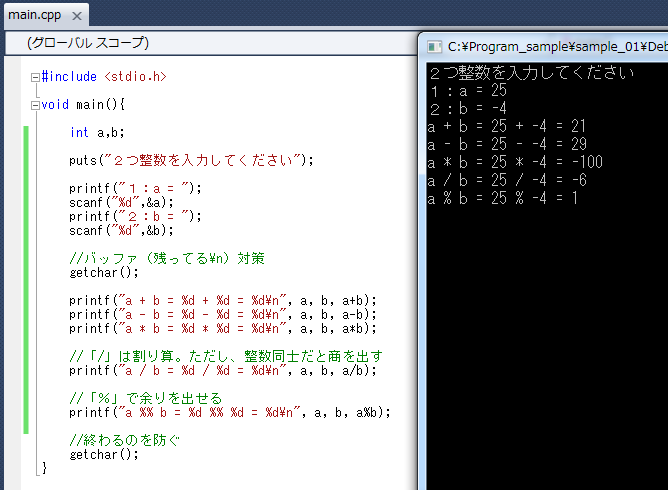
5を2で割ると25ではないの? と思われるかもしれませんが、num1とnum2そしてansは int型の整数を使っているので、小数点以下は切り捨てられ表示されません 。 何度も繰り返しますが、掛け算、割り算、余りの表記はしっかり覚えておきましょう。 比較演算子 約数と倍数 定義 2つの整数 a a , b b について,ある整数 k k を用いて a = bk a = b k と表されるとき, b b は a a の 約数 であるといい, a a は b b の 倍数 であるという。 a = bk a = b k のとき, a = (−b) ⋅(−k) a = ( − b) ⋅ ( − k) でもあるから, b b が a a の
Incoming Term: 割り算の商と余り a-b,




0 件のコメント:
コメントを投稿